When you need a minimum weight spanning tree ...
it's time to implement Prim's algorithm.
So many uses for the set of all edges constituting an MST of a given graph...
Like Kruskal's algorithm, Prim's algorithm finds the set of all edges constituting a minimum weight spanning tree of a given graph. From finding solutions to the "travelling salesman" problem to perfect matching problems, Prim's algorithm and minimum weight spanning trees have an almost infinite number of uses. It is important to note that a single graph may yield many minimum weight spanning trees, but they should all be of the same total weight, meaning the sum of all edge weights of any minimum weight spanning tree from graph G should be equal to the sum of all edge weights of any other minimum weight spanning tree from graph G. For this particular implementation of Prim's algorithm, the application is reliant upon reading from and writing to a file. Please feel free to click on the "VIEW REPOSITORY" button at the bottom of this page in the synopsis section for a full README file which will provide instructions on how to use the application.
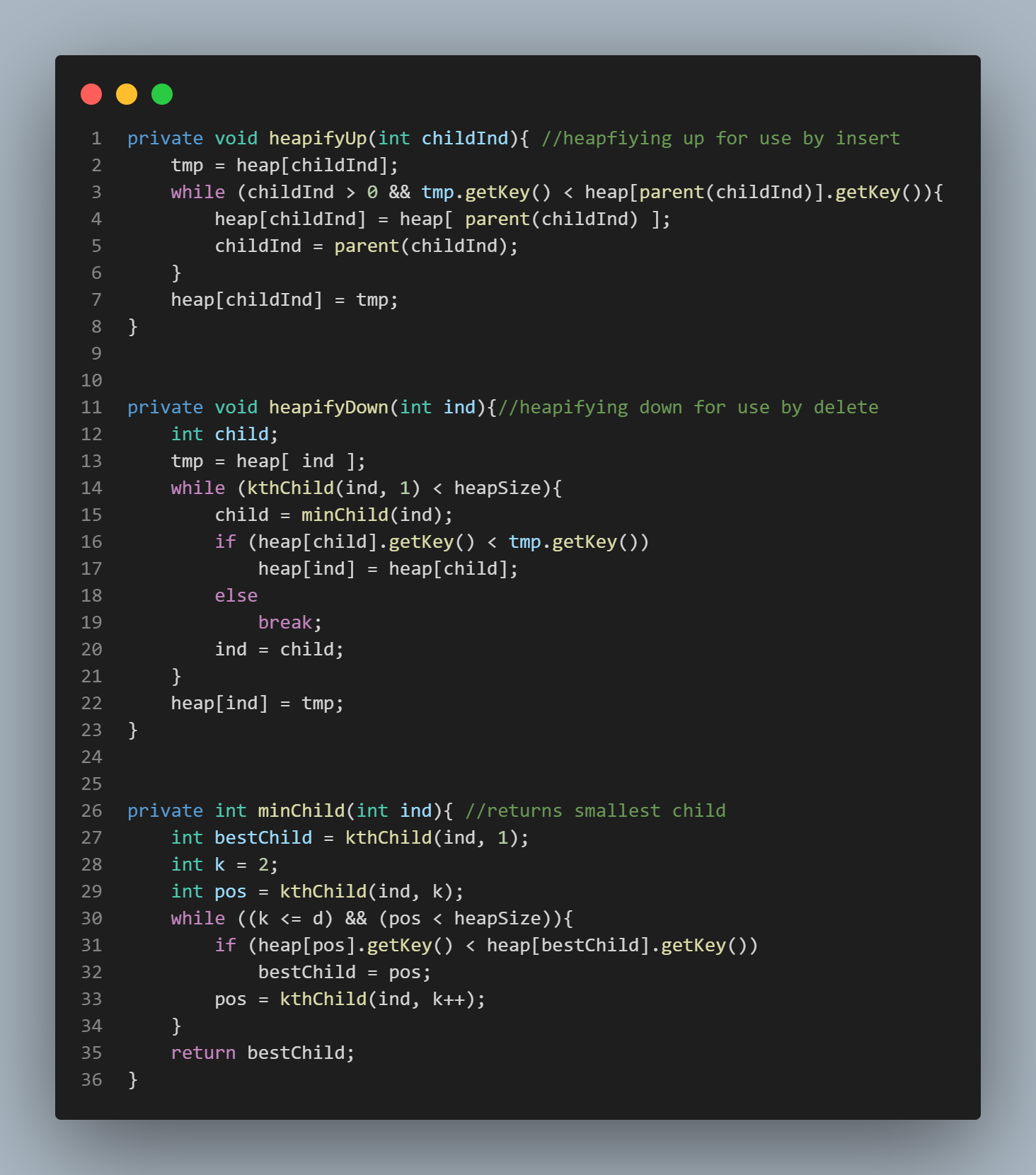
Using a Min Binary Heap as a Priority Queue
In order to achieve a time complexity of O(ElogV) where E = the number of edges in the graph and V = the number of vertices in the graph in a greedy algorithm like Prim's, we need to use a priority queue. The best way to do this is to implement a min binary heap that always maintains the highest priority element as the root node of the binary tree. This means that retrieving the edge in the queue with with the lowest weight simply requires O(1) time (constant time). However, as with any binary heap, after retrieving this prioritized element from the queue and deleting it from the queue, the queue must be re-balanced. This of course requires O(logV) time.
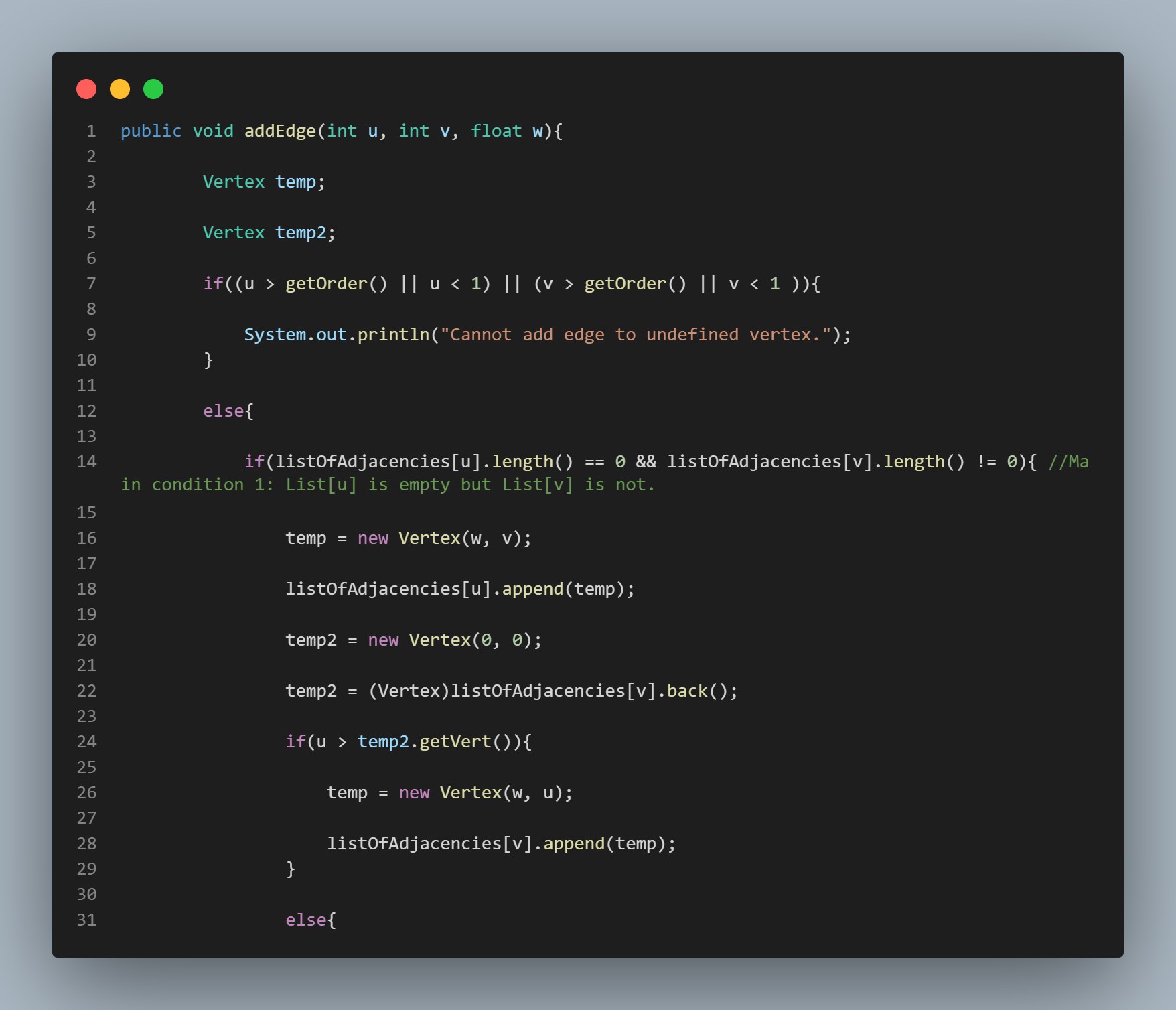
Storing the Graph as an Adjacency List
Storing the graph as an adjacency list is a necessary component of this process. The vertices in the graph are stored as an array of linked lists. For example, index 1 in the array represents vertex 1, and the array element stored at index 1 is itself a linked list composed of all vertices that are adjacent to vertex 1. As is common in graph theory, we use the word "adjacent" to simply mean "connected to vertex 1 by an edge".
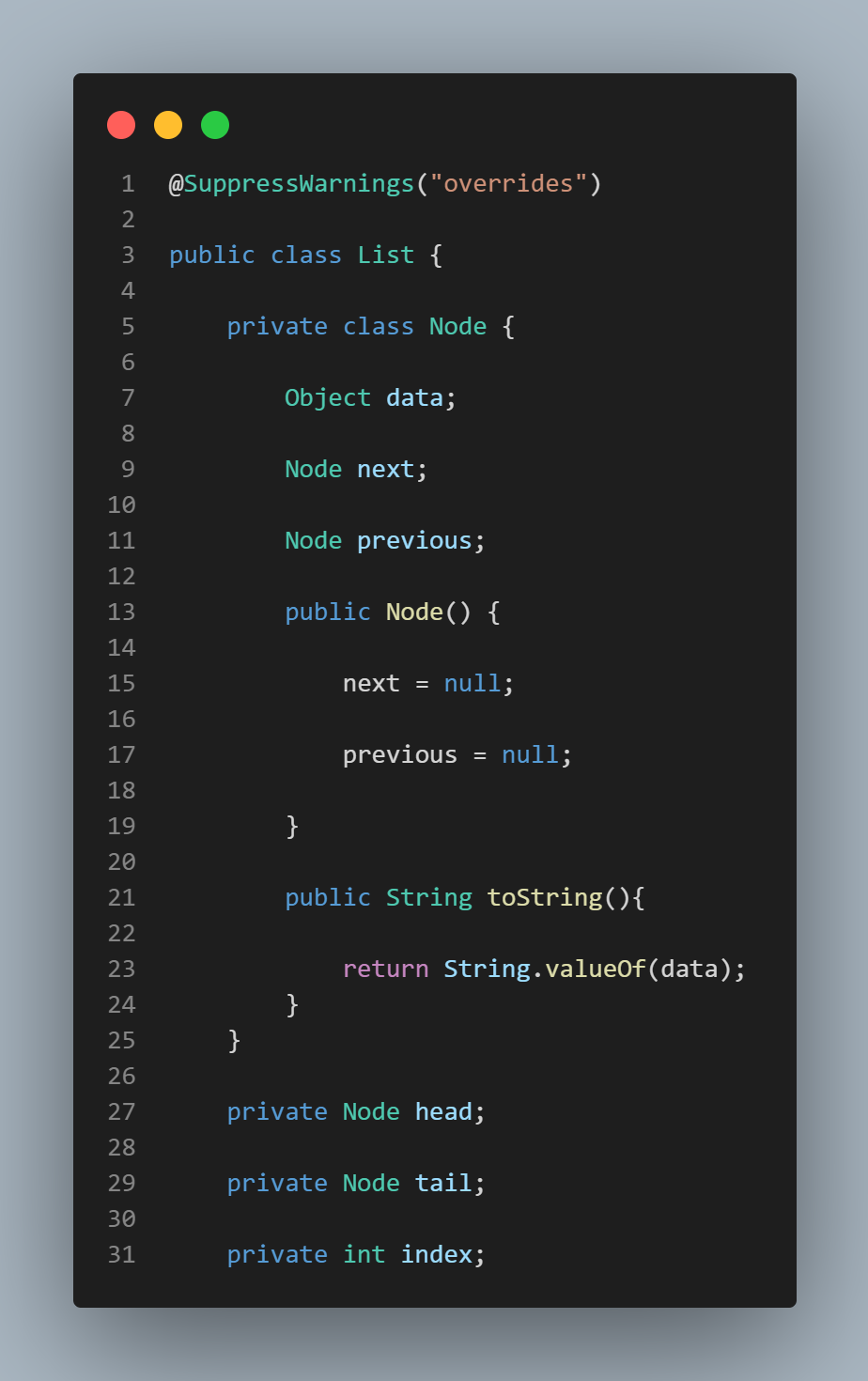
The Tried and True Linked List...
As mentioned above, the data structure used for storing the adjacency lists for this application is a bi-directional (doubly) linked list. Allowing data to be stored in non-contiguous blocks, using a linked list as a storage unit enables us to insert and delete data elements in whatever position we wish. While this property was not actually needed for this application, I chose to use a linked list because I like to keep my skills current for basic commonly used data structure implementations like linked lists. This doubly linked list keeps track of both relationships, i.e., when an edge (u, v) is encountered in the input file, v is added to u's adjacency list and u is also added to v's adjacency list. Because of this, the time complexity of this particular implementation is slightly prolonged. Even though this implementation of Prim's is certainly not as optimal as it could be, I chose certain implementations simply because they represented good exercises for me as a programmer.
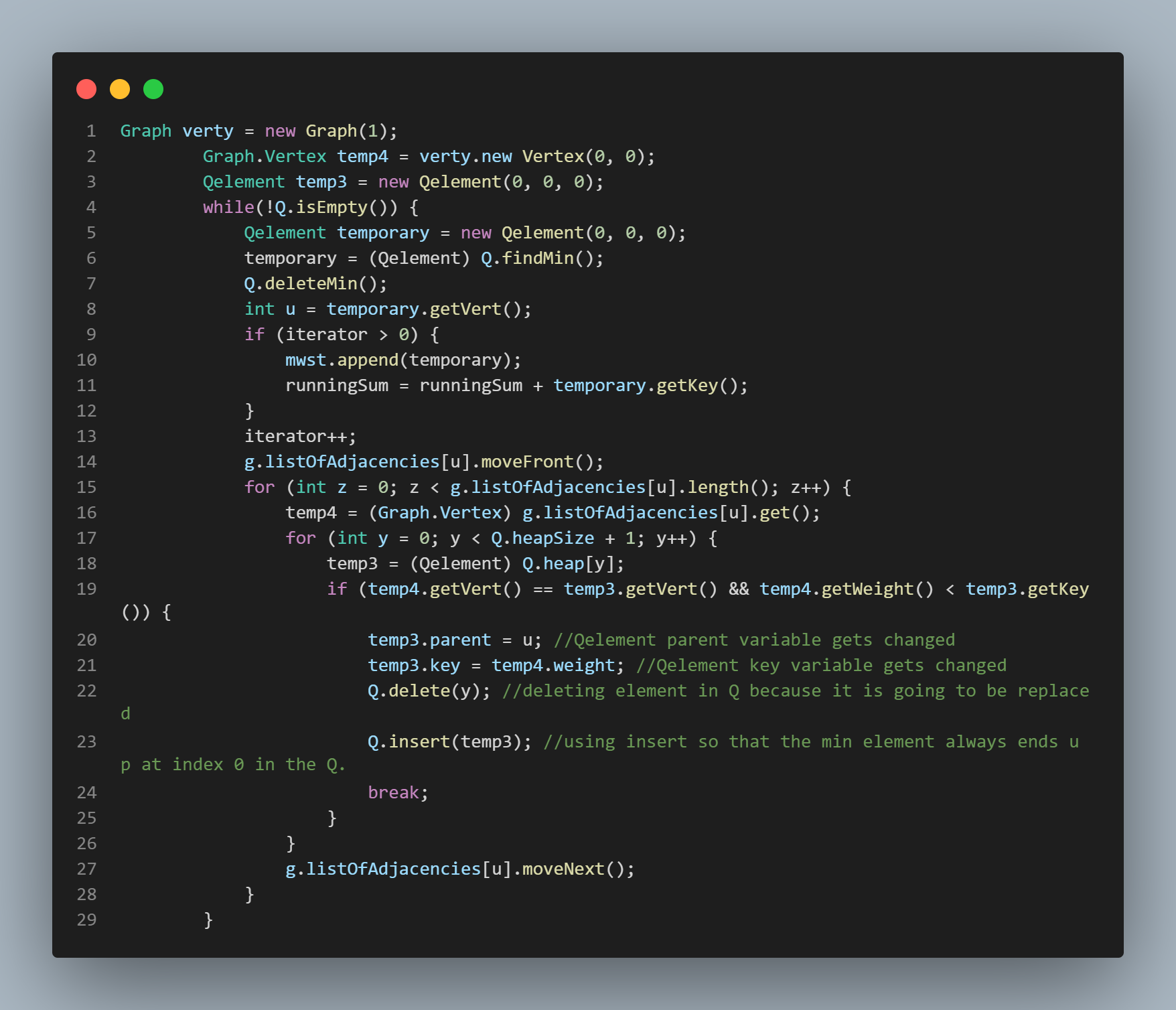
Prim's Algorithm Itself
Prim's algorithm operates by maintaining a queue, (in this particular application's case, a priority queue), of all vertices in the graph. The algorithm is effectively terminated when all vertices have been "deleted" from the queue because this means that each vertex in the graph has been visited, i.e., added to the set of edges representing a minimum weight spanning tree of the given graph. This set of edges is maintained throughout the execution of the algorithm, and the queue is represented by an array of three - tuples, each of which is composed of the vertex number itself, its edge weight in relation to the last vertex under consideration, and its parent vertex. The algorithm picks a starting point node or vertex, and it is from this starting point that the algorithm branches out and greedily populates the set of all edges constituting the minimum weight spanning tree. In this particular implementation of the algorithm, that starting point vertex will always be vertex 1. The algorithm starts by initializing the edge weight of every vertex in the queue to infinity except for the starting point node or root node, which it initializes to 0, and the parent of every vertex in the queue to null, using a loop to perform this operation. It then begins its outer loop by extracting the queue element with the minimum weight. Of course, initially, this is the starting point node, or vertex 1. It then begins an inner loop that iterates through the adjacency list of the vertex that was just extracted from the queue. It updates the edge weight field and parent vertex field of the vertex data objects in the queue that correspond with the vertices it encounters in the adjacency list it is examining. It then adds the vertex under consideration to the minimum weight spanning tree set (only after the completion of the inner loop, of course) which it returns upon the completion of the algorithm as a whole. In this way, Prim's algorithm uses a greedy methodology to construct a minimum weight spanning tree of a given graph.
Synopsis
Extracting the set of all edges composing a minimum weight spanning tree from a given graph and listing them is a very useful tool, and that is what this application accomplishes by implementing Prim's algorithm. Using a minimum binary heap data structure as a priority queue in order to achieve constant time minimum weight edge retrieval, the complete run time of this application is O(ElogV) because each edge must be iterated over, and each time a vertex is extracted from the binary heap, the binary heap must be rebalanced which requires logV time. In the future, I plan to upgrade this application such that the min binary heap is replaced with a Fibonacci tree.
